学过六西格玛的人都知道,在学习假设检验模块的时候,让人印象最深的应该是统计学中出现频率最高,让人又爱有恨的P值吧!有很多人甚至认为,只要掌握了P值,就万事大吉!常常在茶余饭后说:“六西格玛绿带黑带,就学了个P,还没学会?”可见P让多少人为之欢喜,为之烦恼!为之疑惑!
统计学p值的意义:Fisher P值, Neyman-Person 假设检验思想.PNG
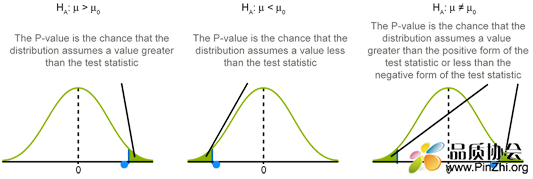
先说说什么是P值:当原假设为真的时候,此结果出现的概率!
从拉普拉斯——->karlPearson——->Fisher P值风靡全球这么多年,Fisher是第一推手,而且还推动了假设检验的思想!在Fisher的假设检验里,是没有备择假设的说法,后来流行的“备择假设”的概念是在一个重要的检验思想里提出的,即Neyman-Person检验思想,这个学派发源于Fisher的思想,但却不太一样。Neyman-Person思想引入了3个不同概念,也是我们现在常用的:
- 引入备择假设。
- 引入两种错误,第一类和第二类错误。
- 使用拒绝域来进行检验。
再说P值应该多大:我们通常使用的0.05,比如P大于0.05 不能拒绝原假设,P小于0.05 拒绝原假设!这算不算在玩数字游戏呢?而且这些结论跟样本量有很大的关系!
问题来了,为什么P是0.05,Fisher先生突然想到0.05,那就一直延续到今天,但还有一种说法:如果是0.1 可接受风险10%=无所谓;如果是0.01 可接受的风险为1%=输不起;所以0.05 正好适合。众说纷纭,总之我们有了标准,而且大家目前都是认可并使用!
最后谈谈P值之应用:很多人可能有疑问,如果我们得出的P值等于0.05,该如何下结论呢?那如果是0.051 或者0.049呢?实际上,我们学习统计学是为了解决问题,而并非为了研究P值本身,就拿0.051来说,P值是判断出现这个值到底有多大可能性,对于0.051来说,比0.05多了千分之一的可能性。你会因为这个千分之一来推翻你既定的假设吗?我想还是要结合实际的情况作出最后的判断,六西格玛的学习者或者应用统计学解决问题者会根据自己的实际情况作出正确的判断!大可不必为了这个P值而纠结是否是0.051还是0.049.单独的P值只能提供有限的信息,用一个略小于0.05的P值来拒绝原假设,或者用一个略大于0.05的P值来不能拒绝原假设都难有说服力。当有其他方法可选时,数据分析不应该以一个简单的P值计算作为结束。
P值的统计显著性知识集
http://www.pinzhi.org/forum.php?mod=viewthread&tid=78821 |