泊松分布(Poisson distribution)
假设你在一个呼叫中心工作，一天里你大概会接到多少个电话？它可以是任何一个数字。现在，呼叫中心一天的呼叫总数可以用泊松分布来建模。这里有一些例子：
- 医院在一天内录制的紧急电话的数量。
- 某个地区在一天内报告的失窃的数量。
- 在一小时内抵达沙龙的客户人数。
- 在特定城市上报的自杀人数。
- 书中每一页打印错误的数量。
泊松分布适用于在随机时间和空间上发生事件的情况，其中，我们只关注事件发生的次数。
当以下假设有效时，则称为“泊松分布”
- 任何一个成功的事件都不应该影响另一个成功的事件。
- 在短时间内成功的概率必须等于在更长的间内成功的概率。
- 时间间隔变小时，在给间隔时间内成功的概率趋向于零。
泊松分布中使用了这些符号：
- λ是事件发生的速率
- t是时间间隔的长
- X是该时间间隔内的事件数。
其中，X称为泊松随机变量，X的概率分布称为泊松分布。
令μ表示长度为t的间隔中的平均事件数。那么，µ = λ*t。
泊松分布的X由下式给出：
泊松分布.GIF
平均值μ是该分布的参数。 μ也定义为该间隔的λ倍长度。泊松分布图如下所示：
泊松分布(Poisson distribution)
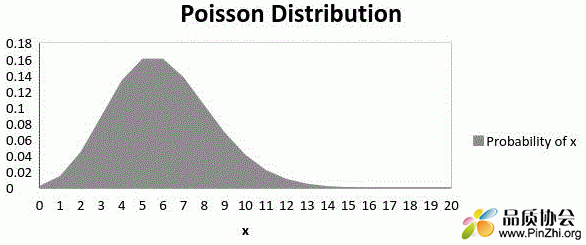
下图显示了随着平均值的增加曲线的偏移情况：
泊松分布(Poisson distribution).GIF
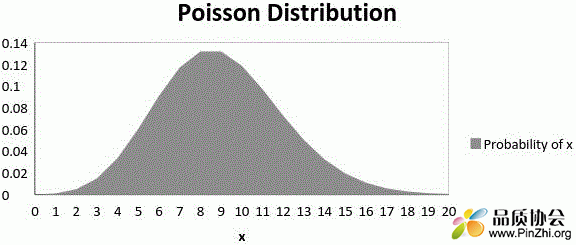
可以看出，随着平均值的增加，曲线向右移动。
泊松分布中X的均值和方差：
均值 -> E(X) = µ
方差 -> Var(X) = µ
二项分布(Binomial distribution)
让我们来看看玩板球这个例子。假设你今天赢了一场比赛，这表示一个成功的事件。你再比了一场，但你输了。如果你今天赢了一场比赛，但这并不表示你明天肯定会赢。我们来分配一个随机变量X，用于表示赢得的次数。 X可能的值是多少呢？它可以是任意值，这取决于你掷硬币的次数。
只有两种可能的结果，成功和失败。因此，成功的概率 = 0.5，失败的概率可以很容易地计算得到：q = p – 1 = 0.5。
二项式分布就是只有两个可能结果的分布，比如成功或失败、得到或者丢失、赢或败，每一次尝试成功和失败的概率相等。
结果有可能不一定相等。如果在实验中成功的概率为0.2，则失败的概率可以很容易地计算得到 q = 1 - 0.2 = 0.8。
每一次尝试都是独立的，因为前一次投掷的结果不能决定或影响当前投掷的结果。只有两个可能的结果并且重复n次的实验叫做二项式。二项分布的参数是n和p，其中n是试验的总数，p是每次试验成功的概率。
在上述说明的基础上，二项式分布的属性包括：
- 每个试验都是独立的。
- 在试验中只有两个可能的结果：成功或失败。
- 总共进行了n次相同的试验。
- 所有试验成功和失败的概率是相同的。 (试验是一样的)
二项分布的数学表示由下式给出：
二项分布(Binomial distribution)
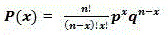
成功概率不等于失败概率的二项分布图：
成功概率不等于失败概率的二项分布图
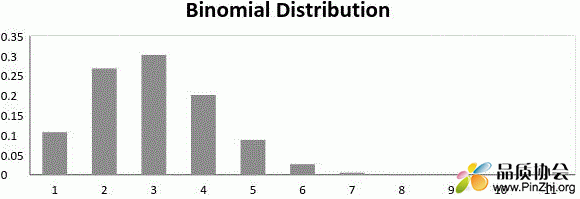
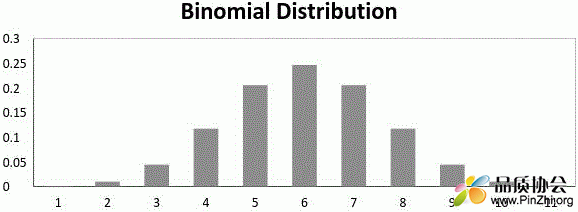
现在，当成功的概率 = 失败的概率时，二项分布图如下：
当成功的概率 = 失败的概率时，二项分布图
二项分布的均值和方差由下式给出：
平均值 -> µ = n*p
方差 -> Var(X) = n*p*q
泊松分布(Poisson distribution)和二项分布(Binomial distribution)的关系和区别
泊松分布在满足以下条件的情况下是二项式分布的极限情况：
1. 试验次数无限大或n → ∞。
2. 每个试验成功的概率是相同的，无限小的，或p → 0。
3. np = λ，是有限的。
正态分布和泊松分布、二项分布的关系及区别
http://www.pinzhi.org/forum.php?mod=viewthread&tid=60679
| 
发表于 2019-3-22 14:49:51
发表于 2023-7-12 15:05:59
发表于 2019-3-23 09:46:17
