误差、不确定度、精密度、准确度、偏差、方差？看完这...

leaper

误差、不确定度、精密度、准确度、偏差、方差？看完这篇就不凌乱了

如何评价分析测试数据的质量，或者说明其测定数据在多大程度上是可靠的，一直是分析工作者和管理者关心和希望解决的问题。在日常分析测试工作中，测量误差、测量不确定度、精密度、准确度、偏差、方差等是经常运用的术语，它直接关系到测量结果的可靠程度和量值的准确一致。
传统的方法多是用精密度和准确度来衡量。但是，通常说的准确度和误差只是一个定性的、理想化的概念，因为实际样品的真值是不知道的。而精密度只是表示最终测定数据的重复性，不能真正衡量其测定的可靠程度。作为一名分析测试人员，这些术语是应该搞清楚的概念，但这些概念互相联系又有区别，也常常使人不知所云。在此略作论述，希望能引起大家讨论。
测量误差
测量误差表示测量结果偏离真值的程度。真值是一个理想的概念，严格意义上的真值是通过实际测量是不能得到的，因此误差也就不能够准确得到。在实际误差评定过程中，常常以约定真值作为真值来使用，约定真值本身有可能存在误差，因而得到的只能是误差的估计值。此外，误差本身的概念在实际应用过程中容易出现混乱和错误理解。按照误差的定义，误差应是一个差值。当测量结果大于真值时，误差为正，反之亦然。误差在数轴上应该是一个点，但实际上不少情况下对测量结果的误差都是以一个区间来表示（从一定程度上也反映了误差定义的不合理），这实际上更像不确定度的范围，不符合误差的定义。
在实际工作中，产生误差的原因很多，如方法、仪器、试剂产生的误差，恒定的个人误差，恒定的环境误差，过失误差，不可控制或未加控制的因素变动等。
由于系统误差和随机误差是两个性质不同的量，前者用标准偏差或其倍数表示，后者用可能产生的最大误差表示。数学上无法解决两个不同性质的量之间的合成问题。因此，长期以来误差的合成方法上一直无法统一。这使得不同的测量结果之间缺乏可比性。
不确定度测量不确定度为“表征合理地赋予被测量之值的分散性，与测量结果想联系的参数”。定义中的参数可能是标准偏差或置信区间宽度。不确定度是建立在误差理论基础上的一个新概念，它表示由于测量误差的存在而对被测量值不能肯定的程度，是定量说明测量结果质量的重要参数。例如，测量结果可能非常接近真值（误差很小），但由于认知不足，人们赋予的不确定度落在一个较大的区间内。也可能实际测量误差很大，但由于分析估计不足，给出的不确定度偏小。一个完整的测量结果，不仅要表示其量值的大小，还需要给出测量的不确定度，表示了被测量值在一定概率水平所处的范围。测量不确定度越小，其测量结果的可疑程度越小，可信度越大，测量的质量就越高，测量数据的使用价值越高。
在实际工作中，测量不确定度可能来源有很多，如定义不完整、取样、基体效应、环境条件、质量和容量器皿的不确定、标准物质、测量方法和程序中的估计和假定以及随机变化等。测量不确定度一般来源于随机性和模糊性，这就使得测量不确定度一般有许多分量组成。在评估总不确定度时，可能有必要分析不确定的每一个来源并分别处理，以确定其对总不确定度的贡献。每一个贡献量即为一个不确定度分量。
不确定度和测量误差的主要区别表

精密度和准确度

精度细分为：准确度：系统误差对测量结果的影响。精密度：随机误差对测量结果的影响。精确度度：系统误差和随机误差综合后对测量结果的影响。

精度是误差理论中的说法，与测量不确定度是不用的概念，在误差理论中，精度定量的特征可用目前的测量不确定度（对测量结果而言）和极限误差（对测量仪器仪表）来表示。对测量而言，精密度高的准确度不一定高，准确度高的精密度不一定高，但精确度高的准确度和精密度都高，精度是精确度的简称。目前，不提倡精度的说法。

我们看待精密度和准确度就如同打靶一样，靶心为真值，设计点为测试结果，分为4种情况：

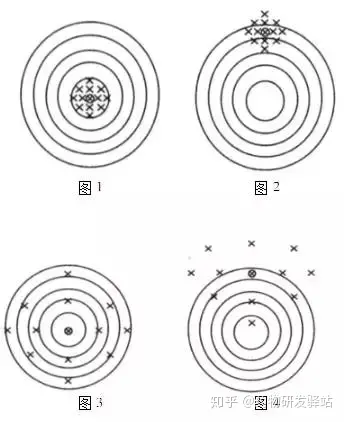
上述 4 种情况中, 第 1 种情况最好, 各测试结果很接近, 精密度好, 平均值与真值很接近, 正确度好。既精密, 又正确, 称为准确度好。这是分析工作者所追求的。

第 2 种情况, 各测试结果接近程度与图 1相同,只是整体从靶心沿半径往外平移一大段距离。表示的期望从靶心移到从外往内第一与第二圈之间。与第 1种情况相比, 精密度不变, 正确度变差了。第 3 种情况, 是图 1 中测试结果以靶心为中心,各自沿半径往外平移不等距离, 象炸开了一样, 变得很分散了。与第 1种情况相比, 正确度不变, 精密度变差了。第 4种情况, 各次测试结果接近程度与图 3 相同, 整体偏移程度与图 2 相同。与第 1 种情况相比,精密度变差, 正确度也变差了。既不精密, 又不正确, 准确度差。

相对标准偏差和方差

偏差：描述的是预测值（估计值）的期望与真实值之间的差距。偏差越大，越偏离真实数据，如下图第二行所示。相对标准偏差（RSD，relative standard deviation）就是指：标准偏差与计算结果算术平均值的比值。相对标准偏差（RSD）=标准偏差（SD）/计算结果的算术平均值（X）*100%，该值通常用来表示分析测试结果的精密度。方差：描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差是衡量源数据和期望值相差的度量值。方差越大，数据的分布越分散，如下图右列所示。

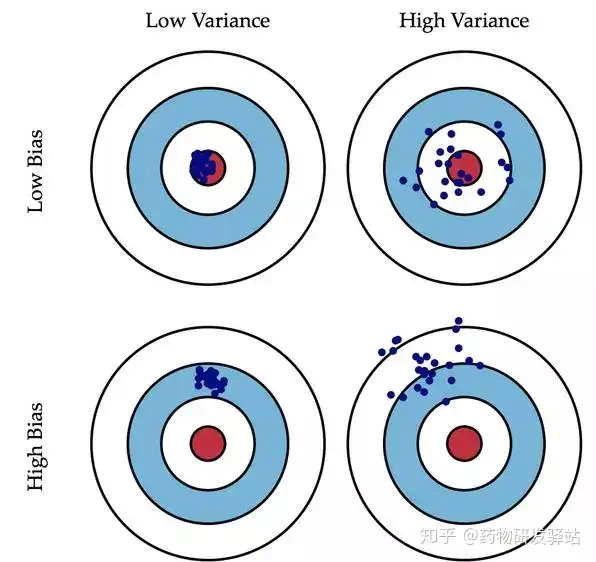
方差分为离散型方差和连续型方差，在统计学意义上，当数据分布比较分散（即数据在平均数附近波动较大）时，各个数据与平均数的差的平方和较大，方差就较大；当数据分布比较集中时，各个数据与平均数的差的平方和较小。因此方差越大，数据的波动越大；方差越小，数据的波动就越小。

当一份分析报告标明了这批数据的偏倚( 表明了正确度) 和相对标准偏差( 表明了精密度) , 也就标明了这批数据的准确度。当分析质量不能满足规范的规定或与数据用户的约定要求时, 需要从人员( 责任心和专业素养) 、 仪器( 特别是仪器的校准) 、 方法( 特别是化验中的样品分解方法) 和环境( 温度、 湿度、 振动、 电磁干扰、 污染等) 4 个方面检查原因并采取相应措施, 把问题解决了才可继续进行分析。

wzp

MSA   做下来不容易

strong_909

楼主解释很详细，谢谢分享！

posl597

感谢 收集分享 好东西

Eric.H

魔兽

ckk594

谢谢分享

一米林夕

被MSA折磨的第三天

tingyu

laker

感谢分享

钻研预检盛世

谢谢分享，

tfan

谢谢分享