主题 解释结果 会话命令 另请参见
在预处理响应示例中,您已决定执行含有 8 个重复的两水平因子试验,以调查三个变量(反应时间、反应温度和催化剂类型)如何影响产量的变异性。使用“分析变异性”确定哪些项(主效应和双因子 交互作用)与产量变异性中的差异显著相关。分析此数据的变异性之前,必须首先执行预处理响应示例以存储响应的标准差和仿行数。
此示例的分析分两步进行。第一步,使用最小二乘回归拟合和简化模型。第二步,确定适当的简化模型后,使用极大似然估计分析简化模型以获得最终模型系数。
步骤 1:使用最小二乘回归估计分析设计
1 完成预处理响应示例。
2 选择统计 > DOE > 因子 > 分析变异性。
3 在响应(标准差)中,输入标准产量。
4 单击项。
5 在按顺序在模型中包括项中,从下拉列表中选择 2。单击确定。
6 单击图形在效应图下方,选中 Pareto、正态和半正态。在每个对话框中单击确定。
会话窗口输出
|
图形窗口输出
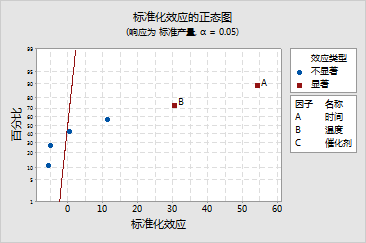
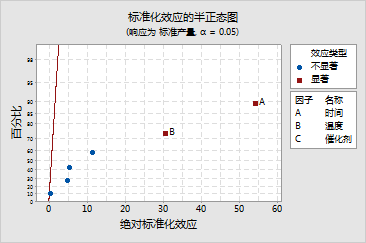
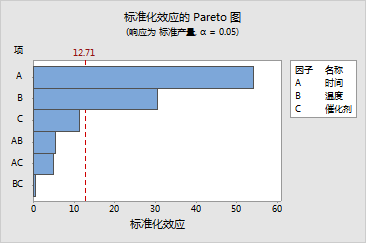
在分析的第一步中,您使用了最小二乘回归来拟合模型。分析数据变异性的一种方法是使用最小二乘回归来确定哪些因子与响应显著相关。确定简化模型后,使用极大似然估计 (MLE) 来确定最终的模型系数。如果项在边界线上表现出显著性,您可能需要检查回归和 MLE 结果,以确定要在模型中保留哪些因子。有关详细信息,请参见 [7]。在许多情况下,最小二乘与 MLE 结果之间的差别很小。
对于本示例,方差分析表提供了主效应和交互作用的汇总。检查 p 值以确定是否有任何显著效应。
结果表明在 0.05 a 水平时,时间和温度都很显著。在 0.05 a 水平时,变量催化剂将近显著。在 0.05 a 水平时,交互作用不显著。在简化模型时, p 值会发生变化。
通过效应的正态图、半正态图和 Pareto 图,可以直观地识别出重要效应,并比较各种效应的相关大小。这些图确认在 0.05 a 水平时,时间和温度都很显著。
此时,应该使用最小二乘回归法简化模型,以确定要在模型中保留哪些项。就本示例的目的而言,含有时间、温度、催化剂、时间与温度、时间与催化剂的模型可作为简化模型。此模型只是可供选择的可能简化模型中的一个。实际上,您可能需要拟合多个模型才能找到合适的模型。逐步变量选择可帮助您查看多个模型。
|
注意 |
如果本示例中的数据是仿行而不是重复,结果和输出可能刚好与上面显示的输出相同。尽管如此,根据分析的变异源,结果可能还是具有不同的实际含义。 |
步骤 2:使用极大似然估计分析简化模型
1 选择统计 > DOE > 因子 > 分析变异性。
2 在响应(标准差)中,输入标准产量。
3 单击选项。
4 在估计法下,选择极大似然。单击确定。
5 单击项。
6 将 BC 从所选项移到可用项。单击确定。
7 单击图形。
8 在效应图下,取消选中 Pareto、正态和半正态。
9 在残差图下,单击三合一。
10 在每个对话框中单击确定。
会话窗口输出
|
图形窗口输出
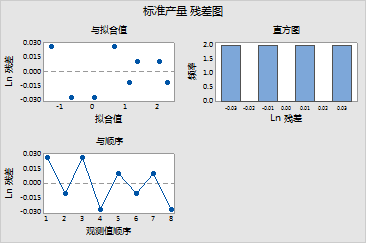
使用最小二乘估计选择适当的简化模型后,可以使用极大似然估计重新拟合模型,以获得最精确的效应和系数。结果表明:
在 0.05 a 水平时,交互作用的统计意义不显著。由于最小二乘估计的 p 值更可靠,因此交互作用仍在模型中。
残差图未显示模式或异常值的证据。
|
注意 |
如果本示例中的数据是仿行而不是重复,结果和输出可能刚好与上面显示的输出相同。尽管如此,根据分析的变异源,结果可能还是具有不同的实际含义。 |